画像処理の高速化（ボックスフィルタ）

目次

• 画像処理の高速化（ボックスフィルタ）
  • 目次
  • 目的
• ボックスフィルタの実装
  • ボックスフィルタのアルゴリズム
  • 画像のデータ構造
  • FIRフィルタにおけるループ構造
  • 演習0
  • 演習1
• ボックスフィルタの高速化
  • スレッド並列化
    • 演習2
  • SIMDによるベクトル化
    • ループ展開
      • カラーループ展開
      • カーネルループ展開
      • 画素ループ展開
      • 演習3
    • 型変換
      • 演習（オプション）
  • アルゴリズムによる高速化
    • 演習4
    • 演習5
    • 演習（発展）
    • 演習（発展）

目的

これまで学んだ高速化手法を応用し，画像処理における基本的な処理であるボックスフィルタを高速化する．なお，ここでは，ボックスフィルタはカラー画像限定とする．また，この演習は，下記のコードを基本として進めるものとする．

• ボックスフィルタ演習コード なお，このコードのうち，ユーティリティ関数(/utils)はimage_processingの課題と同一である．

ボックスフィルタは，移動平均フィルタ（moving averaging filter）や，単に平均値フィルタとも呼ばれる．

ボックスフィルタとは，平滑化フィルタと呼ばれるフィルタの一種であり，移動平均を行うフィルタである．フィルタリングを行う窓関数がボックスであるため，この様に呼ばれる．

画像処理において，平滑化はノイズ除去を始めとして，様々な用途で使用される．そのため，ボックスフィルタの応用例は非常に幅広い．

ボックスフィルタの実装

ボックスフィルタのアルゴリズム

ボックスフィルタでは，注目画素を中心とした正方形の範囲の画素の平均を求めることで，画像を平滑化する．ボックスフィルタの定義式は次の通りである．

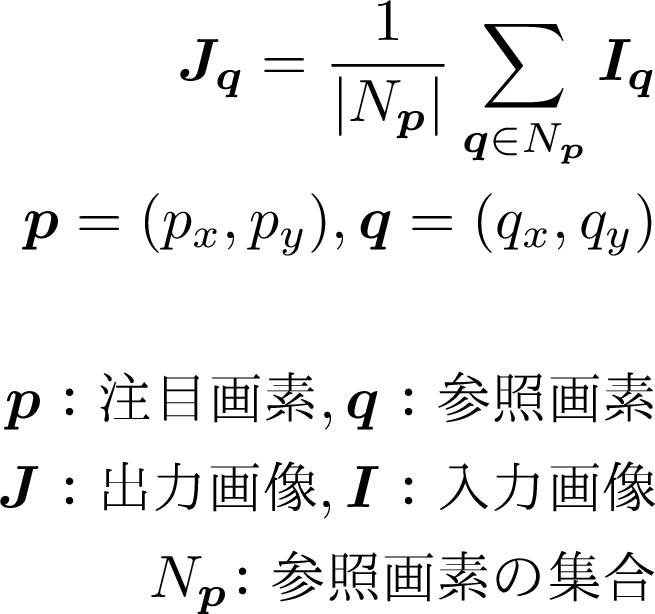
画像のデータ構造

　一般的なカラー画像のデータ構造は，Array of Structure (AoS)である．つまり，画素は，R，G，Bの3つのチャネルを持つ構造体で表現される．そして，それらを配列に格納した状態が一般的な画像のデータ構造である．このとき，左上から列優先で配列に格納されている． 　SIMD演算を用いる場合，AoSではロードを連続して取れないため，チャネル毎を1つの画像に変換して処理を行う．つまり，AoSからStructure of Array（SoA）に変換を行うことが一般的である．

//AoS
Pixel img[width*height]
struct Pixel
{
  unsigned char r;
  unsigned char g;
  unsigned char b;
}

//SoA
struct Image
{
  unsigned char r[width*hight];
  unsigned char g[width*hight];
  unsigned char b[width*hight];
}

FIRフィルタにおけるループ構造

　ボックスフィルタなどの有限の窓を畳み込むフィルタであるFIRフィルタは，カラー画像の場合，5つのループから構成される．それは，外側から順に画素を走査するy，xの二重ループ，参照画素を走査するj，iの2重ループ，チャネルを走査する1重ループである． 　ここでは，これらのループを順に，画素ループ，カーネルループ，カラーループと呼ぶ．なお，カラーループは通常RGBの3つしかないため，すでにループ展開されていることが多い．

for(int y=0;y<heigh;y++) //画素ループ（y方向）
{
  for(int x=0;x<width;x++) //画素ループ（x方向）
  {
    for(int j=0;j<kerne_heigh;j++) //カーネルループ（y方向）
    {
      for(int i=0;i<kernel_width;i++) //カーネルループ（x方向）
      {
        for(int c=0;c<3;c++) //カラーループ
        {
          //img[y+j][x+i][c]への処理
        }
        //一般的には次のようにカラーループは展開されることが多い
        //img[y+j][x+i][0]への処理
        //img[y+j][x+i][1]への処理
        //img[y+j][x+i][2]への処理
      }
    }
  }
}

演習0

ボックスフィルタのコードをコンパイルして実行せよ boxfilterのコードはコマンドライン引数をとることができ，下記のように使える．

./boxfilter 課題番号 繰り返し回数iteration 半径r

また引数を省略した場合は，main直下にデフォルトの値が定義してあり，それを用いる． 課題番号の指定は省略した場合は0版になる． これまでと同様にコメントアウトして使うような場合は指定しなくてもよい．

int main(const int argc, const char** argv)
{
	const int default_loop = 10;
	const int default_r=3;
  const int default_work=0;

fukushima@LetsnoteLV7:~/hpc/boxfilter$ ./boxfilter 4 100 5
work 4: iteration = 100 r = 5

|time(avg) method|time [ms]|
|----------------|---------|
|scalar          |15.3282 ms|
|SIMD            |6.4939 ms|
|scalar separable|7.97769 ms|
|SIMD   separable|7.09138 ms|

|PSNR: method          |PSNR   |
|----------------------|-------|
|PSNR: SIMD            | inf dB|
|PSNR: scalar separable| inf dB|
|PSNR: SIMD   separable| inf dB|

演習1

1. カラー画像におけるボックスフィルタをスカラーで実装せよ．このとき，入力画像のデータ型をfloatとし，画像のデータ構造をSoAに変換する場合の実装を行え．これらの実装については，カラーループは展開せよ．なお，AoSのスカラ実装はサンプルコードで提供している．

   つまり，実装すべきものは下記の1つになる．

   • 入力画像float型のSoAデータ構造におけるスカラ実装である． 実装に関しては，AoS・SoA変換にはsplitやmerge，端点の処理の簡便化にはcopyMakeBorderなど，ライブラリが提供している関数を適時使用せよ．詳細は，ソースコードを参照のこと．

2. カーネル半径rを1から10程度まで変更して，サンプルで提供されているAoS実装と1.の課題で実装したSoA実装の計算時間を計測せよ．また，splitとmergeにかかる計算時間も計測し，フィルタ処理本体とデータ構造変換を含めた場合の計算時間も求めよ．(ここの実験では，処理が単純であるためAoS実装とSoA実装で計算時間に大きな差が表れない場合もある．)

3. AoS実装とSoA実装の計算時間を比較し，計算時間の違いをキャッシュ効率の観点などから考察せよ．また，データ構造変換による計算時間の短縮とデータ構造変換にかかる計算時間より，データ構造変換のトレードオフについても議論せよ．

ボックスフィルタの高速化

スレッド並列化

ボックスフィルタは，FIRフィルタであるため，合計5つのループが存在する．また，任意のループの位置で並列化を行うことが可能である．ただし，ループを並列化する場合，最も外側のループに適用した方が並列化の粒度の観点より効率がいい．

演習2

1. 演習1で実装したスカラーコードをOpenMPでスレッド並列化せよ． 並列化するループは画素ループとし，yループとxループをそれぞれ並列化せよ．

   実装すべきものは下記の2つである．

   • 入力画像float型・スカラ実装・SoA・画素yループ並列化
   • 入力画像float型・スカラ実装・SoA・画素xループ並列化

2. 1.で実装した画素yループ並列化と画素xループ並列化の計算時間を測定し，その結果を比較して最も外側のループを並列化する場合が最も効率が良いことを確認せよ．

3. 画素ループ並列化のコードにおいて，並列化数を変更して計算時間を確認せよ． そして，対応する並列化なし実装とも比較を行い，2.の結果などを踏まえてながら，並列化効率などの観点から，考察せよ．

SIMDによるベクトル化

ループ展開

FIRフィルタをSIMDでベクトル化する場合，以下に示す各ループで展開することが可能である．

カラーループ展開

カラーループは，最も内側のループである．また，他のループに比べて，短いループであるため，ループ展開を既にした状態で記述することが多い．

SIMD命令によるベクトル化をこのループに適用する場合，ベクトル長に対して要素数が少なすぎるため，要素を拡張するようにデータ構造を変換する必要がある．

pixel_before[width*height]
struct pixel_before
{
  float r;
  float g;
  float b;
}

pixel_after[width*height]
struct pixel_after
{
  float r;
  float g;
  float b;
  float padding[5] = {0};
}

このループ展開は，通常のカラーループでは，3個の要素に対して8個の要素に変換して処理するためベクトル化率が悪い．また，最も内側のループであるため，並列化の粒度からいっても細かいため，あまり有効でない．

そのため，カラーのループはsplitして各色ごとに下で記述されているようなループ展開でベクトル化されることが多い．ただし，カラーループのベクトル化のコードが最も簡単に記述しやすい．

また，要素の無駄を省くために要素の拡張を4つにして，SSEで記述してもよい．この場合は，ベクトル長が4となるがベクトル化演算自体の実態が3つしかないため，データがコンパクトになり高速化につながりやすい．

pixel_after_sse[width*height]
struct pixel_after
{
  float r;
  float g;
  float b;
  float padding;
}

//4要素を処理する場合（SSEに相当）
zeroPadding();
for(int y=0; y<img_height; y++){        
  for(int x=0; x<img_width; x++){
    sum[4] = {0};
    weight_sum = 0;
    for(int j=0; j<kernel_height; j++){         			
      for(int i=0; i<kernel_width; i++){
        temp_weight = calcWeight(j, i, y, x);
        sum[0] += temp_weight * I[y+j][x+i][0];
        sum[1] += temp_weight * I[y+j][x+i][1];
        sum[2] += temp_weight * I[y+j][x+i][2];
        sum[3] += temp_weight * I[y+i][x+i][3];// always 0
        weight_sum += temp_weight;
      }
    }
    for(int c=0;i<channels;c++){
      D[y][x][c] = sum[c]/weight_sum;
    }
  }
}

カーネルループ展開

カーネルループ展開は，SIMD演算を使用する場合に最初に思いつきやすい方法である．ただし，後述の画素ループ展開の方が効率がいい．このループ展開では，参照画素を走査するカーネル内の処理（画素のy,xループの次のj,iのループのこと）をSIMD演算によってベクトル化する．

しかし，連続したデータの読み込みは行単位でしか取得することができないので，カーネルの横幅が4ないしは8の倍数でなければ，必ず余り処理が発生する．また，フィルタは原点を中心に左右対称になるように作ることが多く，その結果（2ｘr+1）ｘ（2ｘr+1）：ｒは半径のカーネル，つまり奇数x奇数のカーネルで処理することが多い．この条件では，2のべき乗の倍数に合わすことはできず，必ずあまりが発生する．

余り処理を効率的に行うために，set/gather命令を使用するか，はみ出た部分をマスクして処理の際に必要でない部分の処理を行わないようにするなどの工夫が必要である．もちろん，余り処理をスカラで計算してもよいが，計算効率についてはset/gather命令を使用したものに比べて劣る場合が多い．

この方法では，前処理としてAoSからSoAへの変換が必要である．なお，storeに関しては，スカラとしてstoreを行う．

//4要素を処理する場合（SSEに相当）
convertSoA();
for(int y=0; y<img_height; y++){        
  for(int x=0; x<img_width; x++){
    sum[channels] = {0};
    weight_sum = 0;
    temp_weight_sum[4] = {0;}
    for(int j=0; j<kernel_height; j++){         			
      for(int i=0; i<kernel_width; i+=4){
        temp_weight[4] = {0};
        temp_weight[0] = calcWeight(j, i+0, y, x);
        temp_weight[1] = calcWeight(j, i+1, y, x);
        temp_weight[2] = calcWeight(j, i+2, y, x);
        temp_weight[3] = calcWeight(j, i+3, y, x);
        for(int c=0; i<channels; c++){
          sum[c] += temp_weight[0] * I[c][y+j][x+i+0];
          sum[c] += temp_weight[1] * I[c][y+j][x+i+1];
          sum[c] += temp_weight[2] * I[c][y+j][x+i+2];
          sum[c] += temp_weight[3] * I[c][y+j][x+i+3];
        }
        temp_weight_sum[0] += temp_weight[0];
        temp_weight_sum[1] += temp_weight[1];
        temp_weight_sum[2] += temp_weight[2];
        temp_weight_sum[3] += temp_weight[3];
      }
      residual_processing();
    }
    weight_sum += temp_weight_sum[0];
    weight_sum += temp_weight_sum[1];
    weight_sum += temp_weight_sum[2];
    weight_sum += temp_weight_sum[3];
    for(int c=0;i<channels;c++){
      D[y][x][c] = sum[c]/weight_sum;
    }
  }
}

画素ループ展開

最も外側のループを展開する方法である．なお，データの並びの関係でxを展開するので実際は一つ内側のループである．

これは，ある注目画素における処理をSIMD演算によって並列化するという考え方である．SIMD演算を適用する場合，最も粒状度が大きい方法であり，効果が高い．

なお，画像の横幅が2のべき乗の倍数である必要があり，画像を拡張するか，余り処理が必要となる．しかし，必要な余り処理の総画素数は，カーネルループ展開よりも圧倒的に少なくなる．

この方法では，AoSからSoAへの変換が前処理として必要となる．また，SoAとして保存し，AoSに変換する後処理が必要である．SoAと保存することで，SIMD命令を使用したstoreが可能である．

//4要素を処理する場合（SSEに相当）
convertSoA();
for(int y=0; y<img_height; y++){                					
  for(int x=0; x<img_width; x+=4){
    sum[channels][4] = {0};
    weight_sum[4] = {0};
    for(int j=0; j<kernel_height; j++){         			
      for(int i=0; i<kernel_width; i++){
        temp_weight[4] = {0};
        temp_weight[0] = calcWeight(j, i, y, x+0);
        temp_weight[1] = calcWeight(j, i, y, x+1);
        temp_weight[2] = calcWeight(j, i, y, x+2);
        temp_weight[3] = calcWeight(j, i, y, x+3);
        for(int c=0; i<channels; c++){        	
	         sum[c][0] += temp_weight * I[c][y+j][x+i+0];
	          sum[c][1] += temp_weight * I[c][y+j][x+i+1];
	           sum[c][2] += temp_weight * I[c][y+j][x+i+2];
	            sum[c][3] += temp_weight * I[c][y+j][x+i+3];
            }
            weight_sum[0] += temp_weight[0];
            weight_sum[1] += temp_weight[1];
            weight_sum[2] += temp_weight[2];
            weight_sum[3] += temp_weight[3];
          }
        }
        residual_processing();
        for(int c=0;i<channels;c++){
          D[c][y][x+0] = sum[c][0]/weight_sum[0];
          D[c][y][x+1] = sum[c][1]/weight_sum[1];
          D[c][y][x+2] = sum[c][2]/weight_sum[2];
          D[c][y][x+3] = sum[c][3]/weight_sum[3];
        }
      }
}
convertAoS();

演習3

1. SIMD命令を使用しボックスフィルタを実装せよ． 実装は，前述の画素ループ展開を用いて実装し，スカラで処理行うものと比較せよ． サンプルとしてカーネルループ展開を用いたコードは，ベクトル化，並列化済みのコードが示されている．

   つまり，実装すべきものは次の1つである．

   • 入力画像float型・SIMD実装・SoA・画素yループ並列化・画素ループ展開

2. 1.で実装したコードに対応するスカラ実装，ベクトル化実装の計算時間をカーネルの半径rをr=1から1刻みづつr=16程度まで変更して測定せよ． また，サンプルコードとして提供されているカーネルループ展開についても，同様に計測せよ．

3. 2.の結果より，SIMD実装にしたことによる高速化率や，画素ループ展開とカーネルループ展開の効率の違いや，余り処理の影響などを考察せよ．

型変換

画像のデータ型は，0~255のunsigned char型で格納されているのが一般的である． しかし，何らかしらの処理を行う場合，float型に変換する必要がでてくる． この場合，SIMD命令のunpackとcvt命令を用いることで型変換を実現する． なお，128ビット境界で，データを跨ぐことができないので注意が必要である 256bitのデータをunpackで4本のベクトルに変換すると以下の順序となって分解される．

//md0:  0,  1,  2,  3, 16, 17, 18, 19,
//md1:  4,  5,  6,  7, 20, 21, 22, 23,
//md2:  8,  9, 10, 11, 24, 25, 26, 27,
//md3: 12, 13, 14, 15, 28, 29, 30, 31,

画像処理の場合は大体この状態で十分である場合が多くそのままでよいならそのままで行う． 必要であればpermute命令を使用する．ただし，128ビット境界をまたぐpermute命令はunpack命令などよりも3倍くらい遅い．

//Iは画像データ（画素の配列），データ構造変換でチャネル毎に1枚の画像に変換している．
__m256i md_8u = _mm256_load_si256(img); //unsigned char 32
//md_8u
// 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15,
//16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31

const __m256i zero = _mm256_setzero_si256();
__m256i tmp = _mm256_unpacklo_epi8(md_8u, zero);
__m256i tmpp = _mm256_unpacklo_epi16(tmp, zero);
__m256  md0 = _mm256_cvtepi32_ps(tmpp);

tmpp = _mm256_unpackhi_epi16(tmp, zero);
__m256  md1 = _mm256_cvtepi32_ps(tmpp);

tmp = _mm256_unpackhi_epi8(md_8u, zero);
tmpp = _mm256_unpacklo_epi16(tmp, zero);
__m256  md2 = _mm256_cvtepi32_ps(tmpp);

tmpp = _mm256_unpackhi_epi16(tmp, zero);
__m256  md3 = _mm256_cvtepi32_ps(tmpp);

//md0:  0,  1,  2,  3, 16, 17, 18, 19,
//md1:  4,  5,  6,  7, 20, 21, 22, 23,
//md2:  8,  9, 10, 11, 24, 25, 26, 27,
//md3: 12, 13, 14, 15, 28, 29, 30, 31,

演習（オプション）

1. 画素ループ展開のfloat型実装をuchar型実装に拡張せよ．

   実装に必要なものは，次の1つである．

   • 入力画像uchar型・SIMD実装・SoA・画素ループ並列化・画素ループ展開

2. 1.で実装したuchar型実装と対応するfloat型の計算時間と比較し，メモリI/Oやキャッシュ効率の観点から考察せよ．

アルゴリズムによる高速化

FIRフィルタによる畳み込みは，重み関数を縦横に分解できる（可分性を持つ）場合に限り，縦と横方向の1次元の畳み込みに分割することができる．これをセパラブルフィルタと呼ぶ．

例えば，ボックスフィルタやガウシアンフィルタがそれに当たる．これは，縦方向に1次元で畳み込んだ後に，横方向に1次元で畳み込んだ結果と，2次元で畳み込んだ結果が同じ結果になることを示している．

ボックスフィルタの２次元畳み込みの式は下記となる．

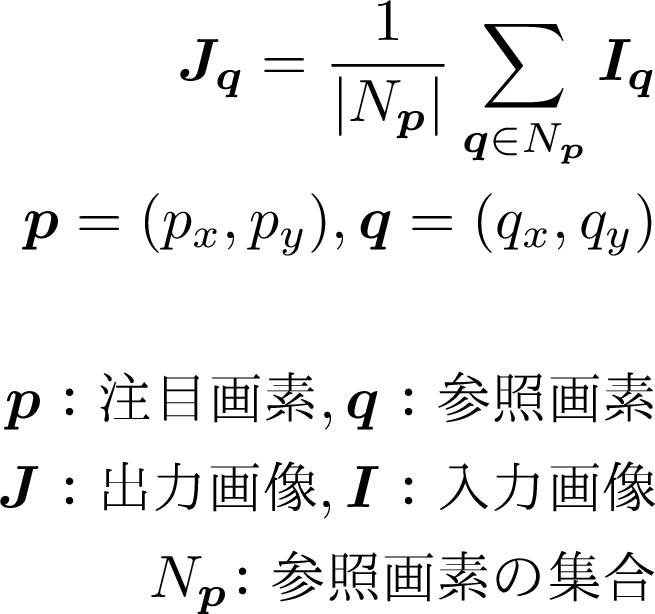
また，これを１次元畳み込みの式に分解すると以下となる．

イメージ図は以下の通り．

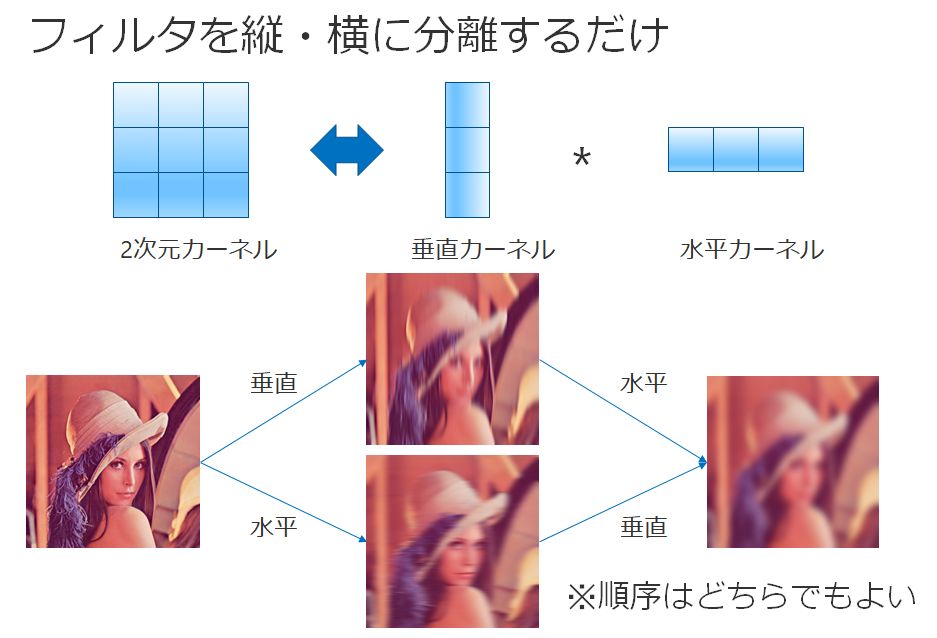
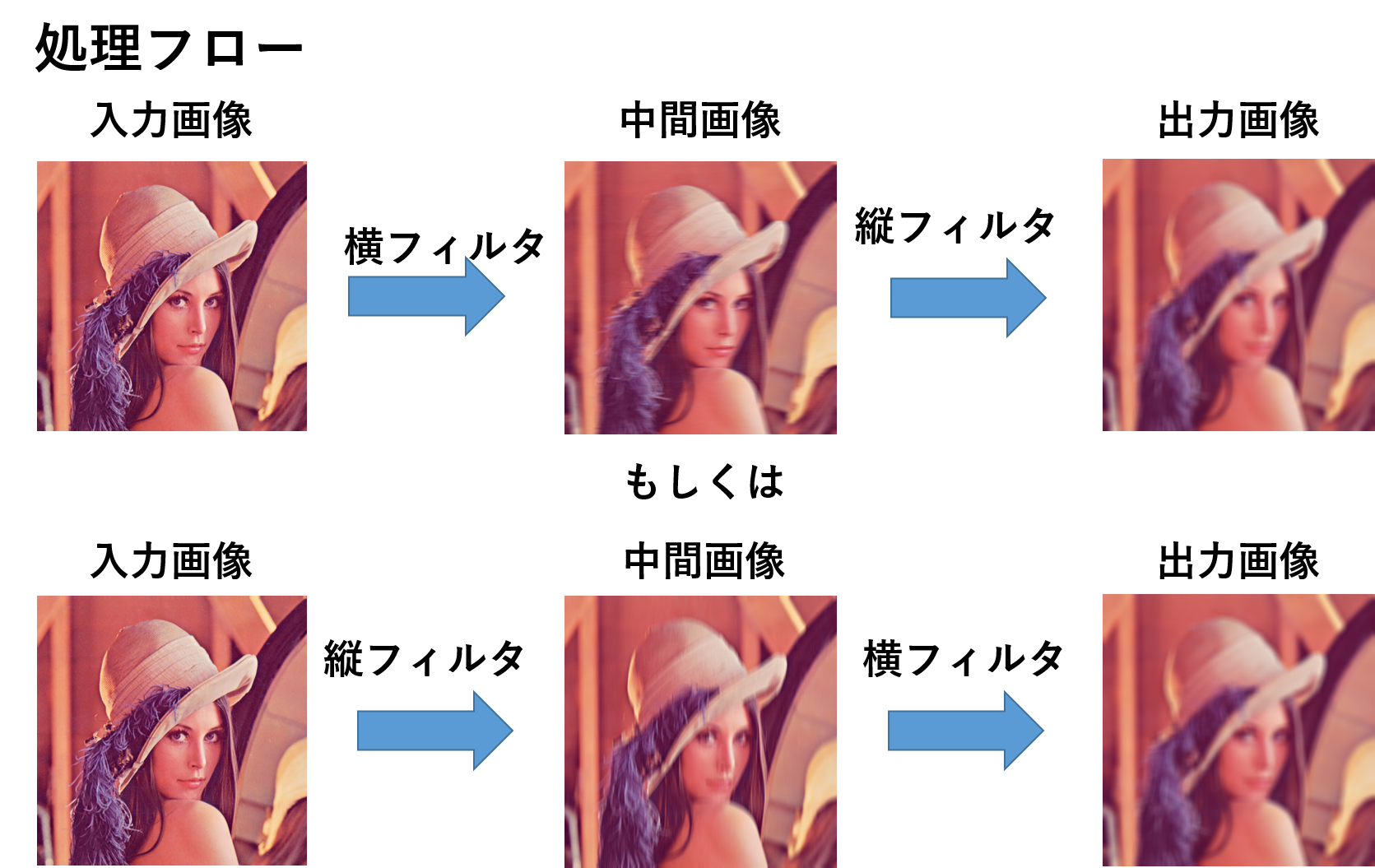
FIRフィルタにおける畳み込みが縦横の2次元から，2回の1次元の畳み込みになるため，計算オーダーが画素当たりO(r^2)からO(r)になるため高速化する．

なお，アルゴリズムとしては画素当たりO(1)のボックスフィルタもあるがベクトル化実装がむつかしいため，本演習では省略した．

演習4

1. SIMD実装を縦，横のセパラブルフィルタに拡張せよ．なお，サンプルとして，スカラーの実装が示されていおり，並列化はすでに適用済みである． 必要な実装は次の1つである．
   • 入力画像float型・SIMD実装・SoA・画素ループ並列化・画素ループ展開
2. rを1から10程度まで変更しながら，スカラ実装，SIMD実装，スカラ・セパラブル実装，1.で実装したSIMD・セパラブル実装の計算時間を測定せよ．
   • なお，rが小さいときはセパラブル実装のほうが遅いことが予想される．もしr=10でもセパラブル実装が遅いときはより大きなrを指定せよ．
   • これはセパラブル実装は2回画像全体を操作するため，通常の実装よりもキャッシュ効率が悪く，計算量の削減量に対してキャッスミスの増加量が上回っているからである．
3. 2.で計測した計算時間より，セパラブルフィルタによる高速化率がO(r)とO(r^2)との関係に従うか調べ，考察せよ．

演習5

演習1から演習5までに次の高速化に寄与する要素の組み合わせを実装してきた． これまでの，演習結果を踏まえて，高速なボックスフィルタの実装について論じよ． また，上記の演習以外で高速化したことがあればここで論ぜよ．

• データ構造：SoA・AoS
• 実装：スカラ実装・SIMD実装
• 並列化：画素ループ並列化・カーネルループ並列化
• ループ展開：画素ループ展開・カーネルループ展開
• アルゴリズム：ナイーブアルゴリズム・セパラブルアルゴリズム
• データ型：uchar型・float型（これはオプショナル）

演習（発展）

これ以降は，時間があった人用．

セパラブルフィルタはスキャン回数を1度だけに減らすことが可能である． 現状では，すべての画素に対して縦フィルタを実行した後にすべての画素に対して横フィルタを実行するように2回の画像全体スキャンがある． これを画像1行の縦フィルタの後に，その1行だけcopyMakeBorderで拡張して，横フィルタを書けるように縦，横，縦，横とインタリーブして進めることで，画像全体をループを1度にしてキャッシュ効率を大幅に向上させることができる． このアルゴリズムを実装せよ．

演習（発展）

これ以降は，時間があった人用．

ボックスフィルタはO(1)までオーダーを落とすことが可能である． O(1)のボックスフィルタを実装せよ．pdf