演習用画像処理用ライブラリの説明

ここでは，提供している画像処理用の簡易ライブラリの説明する． 詳細に関しては，サンプルコードも参照すること．

• 画像処理ライブラリとサンプルコード

なお，実際に研究などで画像処理を行う場合はOpenCVなどの専用のライブラリがあり，これらのライブラリは非常に関数が充実しているためそれを用いるほうが効率的である．

Imageクラス

Matクラスとほんと同じ仕様である． ただし，画像の色情報であるB（青），G（緑），R（赤）を保持するために，channels変数が追加している． 型の変換は，各Imageクラスのコンストラクタで変換すること． データへのアクセスはチャネルが追加されているため，Matでのアクセスとは違った以下のようにアクセスする必要があることを注意すること．

Image_8U a(row, col, channel);
//i行，j列,c番目のチャネルへのアクセス
a.data[a.channels*(i*a.cols + j)+c];

なお，画像の読み込み書き込みは，以下のユーティリティ関数である，readPXM・writePXMで可能である． 保存形式はグレイ画像はpgm，カラー画像はppmである．

フォーマットの詳細は以下のリンクを参照のこと． PNM (画像フォーマット)

データの型の変換は以下のように行う．

Image_8U i8u_1(row, col, channel);
Image_32F i32f(i8u_1); //8Uから32Fへの変換

Image_8U i8u_2(i32f); //32Fから8Uへの変換

チュートリアル課題1

カラー画像を読み込みグレイ画像に変換して，グレイ画像をpgmとして保存したのちに，pgm画像を確認せよ． なお，cvtColorGray関数を用いればよい（cvtはconvertの略）． 画像の確認には，/imgのフォルダを開いてダブルクリックするか，適切なlinuxのコマンドを打てばよい．

チュートリアル課題2

グレイの画像に対して縦横50マスづつ黒く埋める（0を入れる）プログラムを書け， なお，結果はpgmで保存して出力画像を確認せよ．

チュートリアル課題3

カラーで画像を読み込み，緑成分だけ2倍にするプログラムを書け． なお，結果はppmで保存して出力画像を確認せよ． まず，単純に画素値を二倍して出力を確認せよ． そうすると，8bit(uchar)の範囲は0-255のため単純に2倍するとその範囲を超えて値が飽和する． その結果，画素値が想定とは異なった値になっている． その場合は，出力を0-255の値に収まるように以下のようにクリップするとよい．

y=min(max(2*x,0),255);

もちろん以下のように条件分岐で書いてもよい（が，上記のほうが可読性が高いかつ速度も速い）

int val = 2*x;
if(val>255) val = 255
else if(val<0)val=0;
y=mval;

また，この2倍に限定すれば，マイナスになることが想定されないため，以下だけで十分である．

y=min(2*x,,255);

ユーティリティ関数

readPXM・writePXM

readPXM関数は，ppm及びpgmファイルをImage_8Uとして読み込み込む． writePXM関数は，Image_8Uオブジェクトをppm及びpgmファイルとして書き込みを行う．

cvtColorGray

カラー画像をグレー画像に変換する関数． BGRの３チャネルのデータを（B+G+R)/3として１チャネルのグレイ画像に変換する．

copyMakeBorder

フィルタ処理において，端点を処理するために画像を拡張する関数． top，bottom，left，right方向，それぞれを拡張する．

畳み込み演算のコードは，範囲を処理するため，画像の端点では参照画素が外側にはみ出る． 例えば３ｘ３の範囲で平均する場合の(0,0)の画素では，(-1,-1)など存在しない画素にアクセスする． その場合，セグメンテーションフォルトを起こすため，負の値だった場合にどのような処理をするのか正しく例外処理をプログラムに記述する必要がある． 画像の場合はおおむね左上角，上，右上角，左，右，左下角，下，右下角と中央の９領域に分割でき，中央以外は例外処理が必要になる．

このcopyMakeBorder関数は，プログラムとして例外処理をしないために端点を拡張して用いる． この関数は，引数で指定された画像のサイズ分だけ端点の画素を引き延ばして拡張している． その後，増えたサイズの内側だけ処理することで，例外処理を発生させないようにしている．

チュートリアル課題4

copyMakeBorderをカラー画像に対して行い，拡張していない内側の部分だけ黒で塗りつぶせ．

split・merge

splitは，BGRBGR…とインタリーブして画素値が並ぶ状態のImageオブジェクトを各チャネル毎の画像に変換する関数．つまりSoAからAoSの変換を行う． 基本的に画像はこのようなデータ構造をとることが多い．

mergeは，splitで変換した各チャネル画像を持つImageオブジェクトの配列を1つのImageオブジェクトに変換する．

これらの関数は，SIMD命令を使用する際に，データが連続するように変換するためにsplitを行ったり，それを戻すためにmergeを読んだりするために必要である．

---

画像処理の高速化（総合演習用（共通））

下記画像処理を高速化せよ． なお，コード中の下記テスト関数は，簡単なコード，複雑なコードを高速化した例が記述している．

//乗算によるuchar->float変換のSIMD化の例
...
//ガウシアンフィルタの高速化の例
...

ガンマ変換

ガンマ変換とは，画像の輝度値を次式に従い変換する処理である．

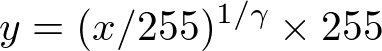
ガンマ変換の実装は，以下のようになる．

const float gamma = 2.2;
Image src;
Image dest;
for(int y = 0; y < height; y++)
{
  for(int x = 0; x < width; x++)
  {
    dest.data[y*width+x] = pow(src.data[y*width+x]/255.f, 1.f/gamma)*255.f;
  }
}

課題0

image-processingのコードをコンパイルして実行せよ このコードはコマンドライン引数をとることができ，下記のように使える．

./image-processing 繰り返し回数iteration

また引数を省略した場合は，main直下にデフォルトの値が定義してあり，それを用いる． 課題番号の指定はこれまでと同様にコメントアウトして使うとよい．

int main(const int argc, const char** argv)
{
	const int default_loop = 10;

fukushima@LetsnoteLV7:~/hpc/image-processing$ ./image_processing 100
iteration = 100

gamma correction
|method|time [ms]|PSNR [dB]|
|------|---------|---------|
|base  | 16.1804|--------|
|opt1. | 0.811683|inf      |
|opt2. | 0.146788|inf      |

課題１

ガンマ変換を高速化せよ． 高速化方法としては，次の方法が挙げられる．

• LUTを使用して演算の削減
• ループ潰し
• ループアンローリング
• スレッド並列化
• SIMDによる実装

注意

image-processing/main.cppのmain関数にプロトタイプ宣言されたガンマ関数がある． void GammaCorrectionがmain関数の下に定義されているので，それをコピーしてGammaCorrectionFastなどの関数を作り直して高速化するとよい．（GammaCorrectionFast1,GammaCorrectionFast2を用意している） また，高速化の結果，バグや数値計算の順序によって演算結果が変わっている可能性があるためPSNR等で正しく挙動しているか確認するとよい．

この注意点は以下の課題でも同じである．

画像の平均・分散計算

画像のすべての画素値の平均値・分散値を計算するのは，リダクション計算となり，効率的に計算するには多少の工夫が必要となる．

課題２

画像画素値の平均値，分散値をそれぞれで求めよ． 高速化方法としては，次の方法によって高速化できる．

• スレッド並列化
• ループ潰し
• ループアンローリング
• SIMDによる実装

なお，ベクトル化などを行った結果，浮動小数点の情報落ちなどによって数値計算の結果が元のコードと異なる場合がある． この場合は，floatではなく桁が大きいdoubleで総和すると，誤差が少ない． この課題では基本はdoubleで総和しており，floatで総和する関数 MeanVarAccFloatと比較しており，平均と分散の結果が違うことが確認できる． また，並列化，ベクトル化により演算順序を変えることでも精度が変わってくる．

総和演算ではこの現象がよく発生し，カハンの加算アルゴリズムなどで対応可能である．ただし速度は大幅に遅くなる．

なお，ベクトル化したほうが，総和の値としては正しい値を返すことが多い．（Pairwise summationを調べると詳細がわかる．） 正しい値かどうかは，doubleで計算した総和結果を正解として，floatで総和を計算したものを比較すればよい．

---